Isotherme zustandsänderung reales gas
$p_2 V_2 = n \; R \; T$ .
und das Gesetz von Boyle und Mariotte (Abschnitt Spezialfälle des allgemeinen Gasgesetzes) mit $T = const$:
$pV = const$.
Für den Vergleich von zwei Volumina bzw.

Bei der isothermen Zustandsänderung entspricht diese Fläche auch der Volumenänderungsarbeit und demnach auch der Fläche im p-V-Diagramm. Da die Enthalpie und die Änderung der inneren Energie gleich Null sind, kann bewiesen werden:
Bei einem reversiblen Prozess kann die Dissipationsarbeit vernachlässigt werden und wir erhalten den Zusammenhang zwischen der Wärme und der verrichteten Arbeit.
Berechnung der Volumenarbeit
Die Fläche unter der Isotherme im p-V-Diagramm entspricht der verrichteten Arbeit W und lässt sich bei Annahme eines idealen Gases mit Hilfe der folgenden Formel berechnen:
Lösen wir die thermische Zustandsgleichung nach p auf
und setzen p in die Gleichung der Volumenänderungsarbeit ein, erhalten wir:
Da sowohl T, als auch m und konstant sind ergibt sich:
Setzen wir für stattdessen ein, erhalten wir schließlich:
Druckänderungsarbeit
Die Druckänderungsarbeit entspricht bei der isothermen Zustandsänderung der Volumenänderungsarbeit.
Das Volumen, der Druck und die Temperatur nehmen einen bestimmten Wert an. Um nun also den Temperaturanstieg zu verhindern kann z.B.
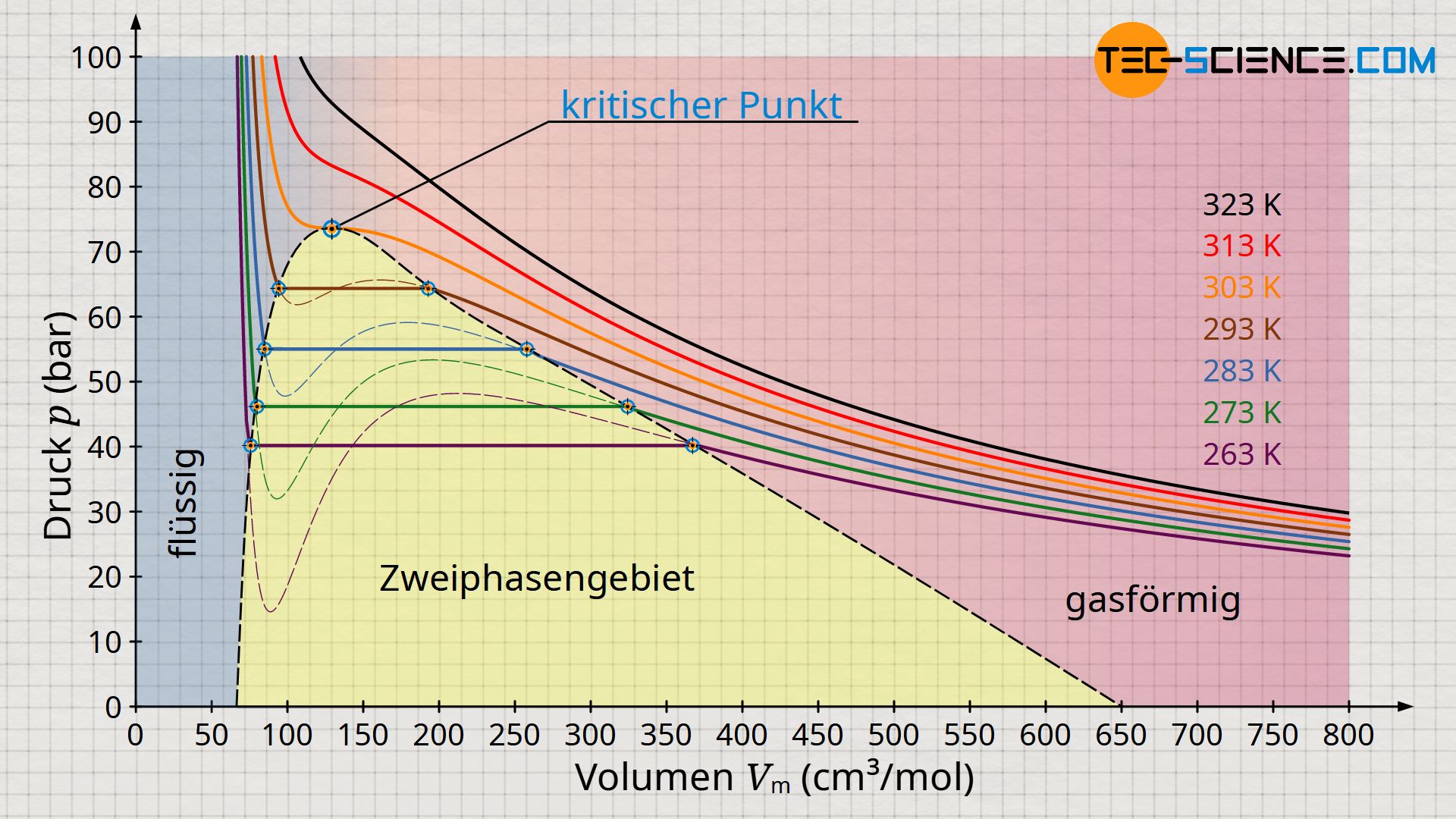
In diesem Beitrag widmen wir uns der isothermen Zustandsänderung. Das bedeutet die p-Achse (y-Achse) und die V-Achse (x-Achse) stellen die Asymptoten dar:
$pV = const$.
Mathematisch ausgedrückt:
$xy = const$.
Die Ableitung von $pV = const$ führt zu:
$p dV + dp V = 0$
$\rightarrow \; \frac{dp}{dV} = -\frac{p}{V}$.
In der obigen Grafik ist deutlich zu erkennen, dass man die Tangente, welche durch den Zustand 1 geht, leicht zeichnen kann.
Das bedeutet, dass Wärme an die Umgebung abgegeben wird. Dies erfordert die Abgabe von Wärme an die Umgebung, um den Druckurtrieb auszugleichen.
Formel: \( P_1 V_1 = P_2 V_2 \)
Hierbei wird das Volumen eines Gases erhöht, ohne die Temperatur zu ändern.
Die Gleichungen können wir durch das Gesetz von Boyle-Mariotte ineinander überführen.
Quiz zum Thema Isotherme Zustandsänderung
5 Fragen beantworten
Entropie
Die in einem System vorhandene Entropie ist von der Aufnahme bzw. Die Formeln für die Entropie sehen wie folgt aus:
$S_2 - S_1 = \int_1^2 \frac{dU + p \; dV}{T} = \int_1^2 \frac{p \; dV}{T}$.
Einsetzen der thermischen Zustandsgleichung (nach $p$ aufgelöst):
$S_2 - S_1 = \int_1^2 \frac{ m\; R_i \; T \; dV}{V \; T}$.
Alle konstanten vor das Integral ziehen ($m$, $R_i$, $T$):
$S_2 - S_1 = m \; R_i \int_1^2 \frac{dV}{V}$.
Integral auflösen ergibt die Änderung der Entropie mittels Volumenverhältnis:
$S_2 - S_1 = m \; R_i \; \ln(V_2) - \ln(V_1) = m \; R_i \; \ln (\frac{V_2}{V_1})$.
Einsetzen des Gesetzes von Boyle und Mariotte $\frac{p_1}{p_2} = \frac{V_2}{V_1}$ ergibt die Änderung der Entropie mittels Druckverhältnis:
$S_2 - S_1 = m \; R_i \; \ln (\frac{p_1}{p_2})$.
Die Entropie lässt sich in einem T,S-Diagramm darstellen.
Durch die Einführung der Masse m des Gases und der spezifischen Gaskonstanten kann mithilfe der Beziehungen
die Volumenarbeit bei isothermer Expansion umgeformt werden in:
Diese Arbeit ist gleich der dem Gas zugeführten Wärme, die dieses benötigt, um seine innere Energie bei der Expansion konstant zu halten.
Es handelt sich bei der Volumenänderungsarbeit um Arbeit, welche vom System abgegeben wird und demnach negativ ist.
Innere Energie / Enthalpie / Wärme
Bei der iosthermen Zustandsänderung $T = const$ ändert sich die innere Energie und die Enthalpie nicht, da diese temperaturabhängig sind:
$U_2 - U_1 = \int_1^2 m \; c_v \; dT = 0$
und
$H_2 - H_1 = \int_1^2 m \; c_p \; dT = 0$.
Die Änderung der inneren Energie und die Änderung der Enthalpie ist bei der isothermen Zustandsänderung gleich Null.
Daraus folgt für die Berechnung der Wärme aus der Formel für die Änderung der inneren Energie:
$U_2 - U_1 = Q + W_V + W_{diss} = 0$.
Für einen irreversiblen Prozess ergibt sich damit für die Wärme:
$Q = -W_V - W_{diss}$.
Für einen reversiblen Prozess mit $W_{diss} = 0$ ergibt sich:
Es folgt für die Berechnung der Wärme aus der Formel für die Änderung der Enthalpie:
$H_2 - H_1 = Q + W_t^{rev} + W_{diss} = 0$.
Für einen irreversiblen Prozess ergibt sich damit für die Wärme:
$Q = -W_t^{rev} - W_{diss}$.
Für einen reversiblen Prozess mit $W_{diss} = 0$ ergibt sich damit für die Wärme:
$Q = -W_t^{rev}$.
Da es sich außerdem um einen reversiblen Prozess handelt, kann die Dissipationsarbeit vernachlässigt werden.
direkt ins Video springen
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Thermische Zustandsgleichung
Setzen wir die konstant bleibende Temperatur in das ideale Gasgesetz ein, dann folgt daraus:
- n = Stoffmenge [mol]
- R = universelle/molare Gaskonstante [8,3144598 ]
- T = Temperatur [K]
- = individuelle/spezifische Gaskonstante
- m = Masse [kg]
- p = Druck [Pa]
- V = Volumen []
für
Anders als bei der isochoren und isobaren Zustandsänderung ist dieser Term nun umgekehrtproportional und als Gesetz von Boyle-Mariotte bekannt.
Es soll sich hierbei um einen nicht-adiabten Kolben handeln. Sie kann durch Auszählen der Fläche oder durch Integration berechnet werden.
Isotherme Zustandsänderungen
Nach dem 1.
Die Temperatur steigt ebenfalls an. Um den Energieerhaltungsgesetz zu gehorchen, muss das System Wärme von der Umgebung aufnehmen.
Formel: \( W = nRT \ln \left( \frac{V_f}{V_i} \right) \)
In einem Druck-Volumen-Diagramm (P-V-Diagramm) verläuft eine isotherme Kurve exponentiell.
Vom Punkt $V_1$ aus wird in Richtung der positiven $V$-Achse eine Strecke der Länge $V_1$ eingezeichnet (schwarze Linie). Das bedeutet also, dass die Fläche unter der Kurve im T,S-Diagramm genau so groß ist, wie die Flächen im p,V-Diagramm. Dadurch entsteht Wärmeenergie, welche abgeführt werden muss.
Die innere Energie ändert sich durch Wärmetransport oder Verrichtung von Arbeit.
Schauen wir uns beide an.
Quiz zum Thema Isotherme Zustandsänderung
5 Fragen beantworten
Isotherme Expansion und Kompression
Bei der isothermen Expansion wird einem Gas Wärme zugeführt, wodurch es sich ausdehnt und Volumenarbeit verrichtet.
Ein Beispiel für einen komplexen thermodynamischen Vorgang ist der Kreisprozess eines Verbrennungsmotors. Das bedeutet, dass die Temperatur bei der Zustandsänderung konstant bleibt. Hier sind zehn Arten von isothermen Prozessen, die in Gasen vorkommen können:
Bei der isothermen Kompression wird das Volumen eines Gases reduziert, während seine Temperatur konstant bleibt.
Bei der isothermen Zustandsänderung bleibt die Temperatur konstant. Im Allgemeinen ändern sich dann Druck und Volumen des Gases.
Isotherme Expansion und Kompression
Nach dem 1. Die Zustandskurve im p-V-Diagramm entspricht einer Hyperbel und im T-s-Diagramm ist sie eine Konstante. $p_1 V_1 = n \; R \; T$ .
$p_2 V_2 = m \; R_i \; T$ bzw.